CATALOG

    WebGL Programing Guide 学习笔记

    之前我们已经了解了：

    在真实世界中，物体在光线照射下的表现十分重要。这次我们就来学习下 WebGL 中光照的基础知识。

    shading

    首先光线照射不光会造成“阴影”，物体表面的颜色也会发生变化，这就是 shading。

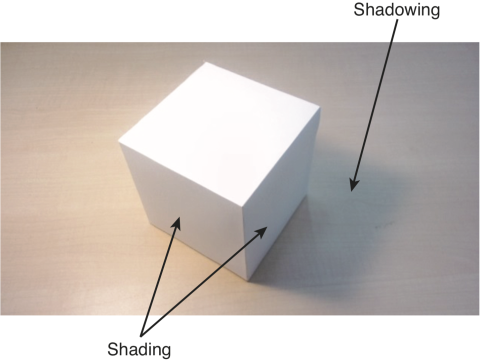
    shading 和 shadow

    shading 和 shadow

    影响因素显然有两个：光源类型以及物体表面的反射情况。

    光源类型

    除了熟悉的平行光例如阳光和点光源，环境光源是光线被其他物体表面反射，再到达目标物体表面的一种光源模型。 书中举了一个很常见的例子：在夜晚打开冰箱门，整个房间都变亮了一点。

    光源类型

    光源类型

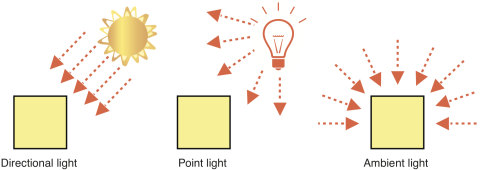
    下面来看看物体表面的反射情况。

    漫反射

    漫反射

    漫反射

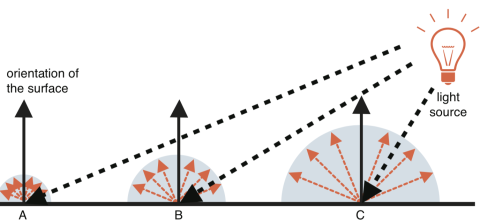
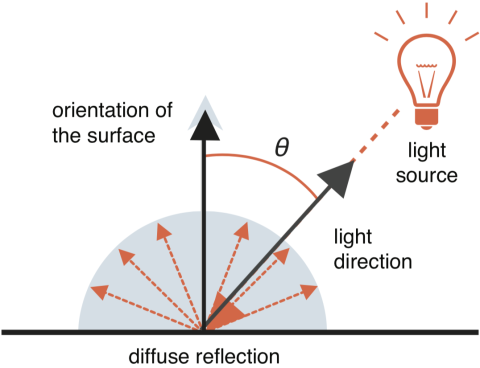
    漫反射表面颜色计算公式如下。当 θ 为90度也就是光源照射方向平行于物体表面，表面颜呈现黑色，这也符合我们的常识。

    〈surface color by diffuse reflection〉 =
    〈light color〉 × 〈base color of surface〉 × cosθ

    但是在实际应用中，θ 是很难直接得到的。相对的，光源方向和物体表面的方向很容易得到：

    cosθ = 〈light direction〉 • 〈orientation of a surface〉

    只要得到垂直于物体表面的法向量和光源方向向量，就能计算出 cos θ：

    cos θ 的计算

    cos θ 的计算

    这里涉及一个简单的线性代数知识，如果 n 和 l 都是单位向量，即模为 1，cos θ 就是两个向量点乘的结果：

    n • l = |n| x |l| x cos θ

    在 fragment shader 中，使用 GLSL ES 提供的一系列内置工具函数，应用以上公式，就可以计算出最终物体表面的颜色：

    attribute vec4 a_Color;
attribute vec4 a_Normal; // 法向量
uniform vec3 u_LightColor; // 光源颜色
uniform vec3 u_LightDirection; // 光源方向向量，标准向量
varying vec4 v_Color;

vec3 normal = normalize(a_Normal.xyz);
float nDotL = max(dot(u_LightDirection, normal), 0.0);
vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;
v_Color = vec4(diffuse, a_Color.a);

    这里有一个注意点，在计算光源方向和法向量的点乘结果时，我们保证了最小值为0。 这是由于当结果小于0时，说明夹角大于 90 度，光源处于物体表面的背后，颜色显然就是黑色了。

    环境反射

    在实际场景中，背对光源的表面也不一定为纯黑，来自墙壁，地面等其他物体的反射光线投到物体表面，也会使表面颜色发生改变，这就是环境反射。

    环境反射

    环境反射

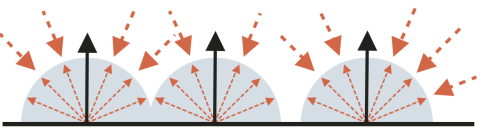
    相比漫反射，不需要考虑光源和表面的夹角。

    〈surface color by ambient reflection〉 =
    〈light color〉 × 〈base color of surface〉

    加上之前的漫反射：

    uniform vec3 u_AmbientLight;
vec3 ambient = u_AmbientLight * a_Color.rgb;

v_Color = vec4(diffuse + ambient, a_Color.a);

    镜面反射

    这部分「WebGL Programing Guide」这本书并没有涉及。其实学的时候是和另一本「Professional WebGL Programming: Developing 3D Graphics for the Web」一起同步着看的。在这本书中，介绍了 Phong reflection model 又被称作 ADS（“Ambient, Diffuse, and Specular”）光线模型。在简化的场景以及材质下，其实可以不用考虑镜面反射。

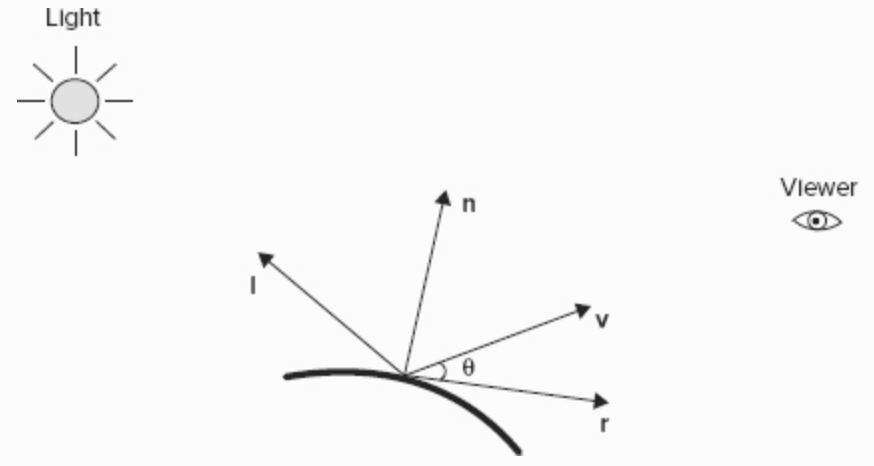
    Specular Reflection

    除了物体表面的法向量 n，还有和光照方向相反的向量 l，而 r 是光线反射的方向向量。

    具体到公式，α 代表了材质的 shininess

    I = ks x Is x max(r · v, 0)^α

    其中 r 的计算可以通过 l 和 n 得到：

    r = 2(l · n)n-l

    但是 GLSL 中可以直接使用内置函数 reflect 得到镜像向量，唯一要注意的是 l 是与光线方向相反的：

    vec3 reflectionVector = normalize(reflect(-vectorToLightSource, normalEye));

    最后实现一遍公式：

    vec3 viewVectorEye = -normalize(vertexPositionEye3);
float rdotv = max(dot(reflectionVector, viewVectorEye), 0.0);
float specularLightWeightning = pow(rdotv, shininess);

    法向量的计算

    之前法向量都是不变的，在实际场景中，当应用了变换矩阵，做出了平移旋转缩放之后，如何通过变换矩阵计算当前的法向量呢？

    这里需要使用逆转置矩阵。顾名思义，先对变换矩阵得到逆矩阵，再交换行列就得到：

    normalMatrix.setInverseOf(modelMatrix);
normalMatrix.transpose();

    变换之后的法向量只要左乘逆转置矩阵即可：

    vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal))

    光线方向计算

    之前在漫反射中讨论的光线方向都是一致的，换言之，对于同一个表面，接收到的是平行光。 而在实际生活中光源常常是一个物体，例如电灯泡会向四周发射光线，这样同一个表面上不同的点接收到的光线方向也就不一样了。

    per-vertex

    对于每一个 vertex，需要先左乘变换矩阵得到相对世界坐标，然后与光线方向向量相减，得到该 vertex 接收到的光线方向。

    vec4 vertexPosition = u_ModelMatrix * a_Position;
vec3 lightDirection = normalize(u_LightPosition - vec3(vertexPosition));

    但是仔细观察会发现这样计算出的效果存在瑕疵，尤其是在球体上十分明显。这是由于我们针对 vertex 进行计算，随后会经过线性插值得到每个 fragment 的值。

    per-vertex 计算效果

    per-vertex 计算效果

    「WebGL Programing Guide」这本书并没有详细介绍问题的原因，相比之下「Professional WebGL Programming」比较详细的给出了解释。

    per-vertex 又被称为 Gouraud Shading，在下面的场景中，P0 应该是高光部分，但是由于在该模型下，P0 根据三个 vertex 平均得到，因此最高光的部分就丢失了。

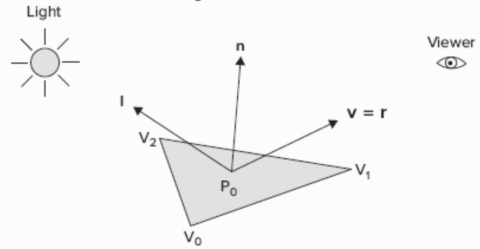
    损失的高光部分

    损失的高光部分

    per-fragment

    因此为了得到更真实的渲染效果，需要针对每个 fragment 进行计算。 这就需要将 shading 计算逻辑从 vertex shader 中挪到 fragment shader 中。 这种计算方式也叫做 Phong shading。

    在Shader 基础知识中，我们知道在两个 shader 之间传递变量需要用到 varying。

    在 vertex shader 中计算好法向量，连同物体表面颜色一起传递过去。 有一点需要注意，计算出的 vertex 坐标也就是 v_Position 在到达 fragment shader 前会先经过线性插值，毕竟 vertex 比 fragment 数量少的多得多。

    v_Position = vec3(u_ModelMatrix * a_Position);
v_Normal = normalize(vec3(u_NormalMatrix * a_Normal));
v_Color = a_Color;

    真正的计算放在 fragment shader 中，这里的 v_Position 已经是线性插值之后的了。 v_Normal 和 v_Color 也是一样：

    vec3 normal = normalize(v_Normal);
vec3 lightDirection = normalize(u_LightPosition - v_Position);
float nDotL = max(dot(lightDirection, normal), 0.0);
vec3 diffuse = u_LightColor * v_Color.rgb * nDotL;
vec3 ambient = u_AmbientLight * v_Color.rgb;
gl_FragColor = vec4(diffuse + ambient, v_Color.a);

    比如对于每个 fragment 处的法线：

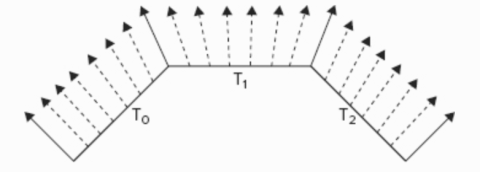
    通过插值得到的法线

    通过插值得到的法线

    当时看到这里我发现了一个问题，那就是对于 GLSL 内置函数 normalize 的使用。从 vertex-shader 中传递过来的 v_Normal 不是已经通过 normalize 了么，为啥到了 fragment shader 中还要再调用一次呢？

    原因是线性插值会改变向量的长度，比如下面的 n1。而且不难发现，如果 n0 或者 n2 没有先经过 normalize，插值后得到的 n1 不光是长度方向都会改变。

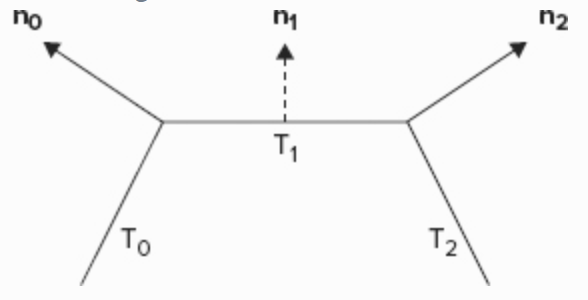
    Spot lights

    除了平行光和点光源，还有一种特殊的光源：点光束，类似舞台上的聚光灯。

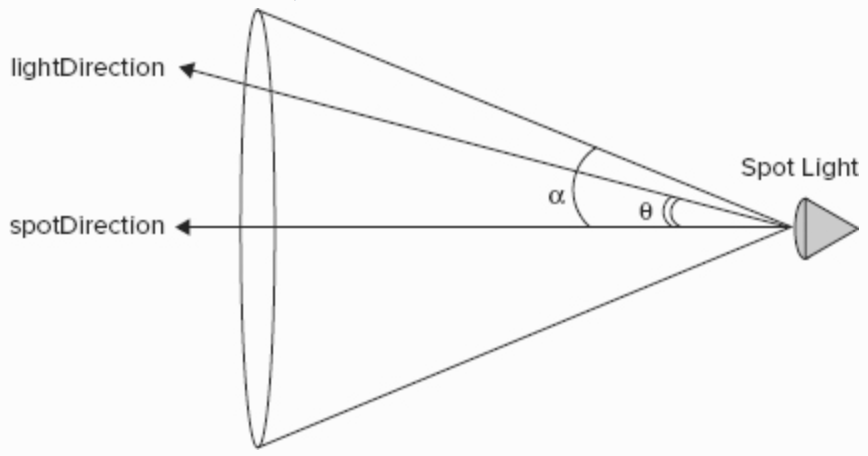
    通过公式得到每个角度下的光照系数：

    spotEffect = (cos θ) ^ spotExponent = (spotDirection · lightDirection) ^ spotExponent

    但是要注意，这个光束是有夹角的，只有在角度范围内才需要乘以这个系数：

    const float spotExponent = 40.0;
const float spotCosCutoff = 0.97; // 14 度对应的值
float spotEffect = dot(normalize(uSpotDirection), 
    normalize(-vectorToLightSource));
// 光束范围
if (spotEffect > spotCosCutoff) {   
    spotEffect = pow(spotEffect, spotExponent);
    // 省略同样的计算漫反射和镜面反射过程
    lightWeighting = 
        spotEffect * uDiffuseLightColor * diffuseLightWeighting +
        spotEffect * uSpecularLightColor * specularLightWeighting;

    光线的衰减

    遵循如下公式，r 是距离。

    值得注意的是，这部分计算不能放在 vertex shader 中，尤其是距离。 因为不能依赖线性插值，例如在粗糙的物体表面，每个 fragment 到光源的距离并不是线性变化的。

    利用内置函数 length 可以得到向量的长度：

    float distance = length(vec3(vLightPositionEye3 - vPositionEye3));

    Light Map

    如果对象，光源都是静态的，那完全可以在建模时就计算好，不用实时计算。 和材质一样，光线照射情况也可以存储在 texture 中。

    uniform sampler2D uSamplerBase;
uniform sampler2D uSamplerLight;
 
void main() {
    vec4 baseColor = texture2D(uSamplerBase, vTexCoordinates);
    vec4 lightValue = texture2D(uSamplerLight, vLightCoordinates);
    gl_FragColor = baseColor * lightvalue;
}

    总结

    现在我们知道了光线照射下物体表面颜色的计算方法。是时候将多个简单 3D 对象组合成一个复杂物体了。