噪声的艺术

最近学习「the book of shaders」，了解到这种完全依靠 fragment shader 绘制，而不需要 vertex shader 过多参与的技术被称作“Pixel-Shader”。

在上一篇「绘制 Pattern」中学习了 Pattern 的绘制思路以及一些基本形状的绘制方法。而很多艺术效果中，完全规则的图形反而会很生硬，噪声的应用使得图案变得更加“自然”，因此应用是十分广泛的。

模拟随机

为了实现噪声效果，肯定需要用随机函数。而 GLSL 中并没有类似 random() 这样的内置函数，这就需要我们模拟这种随机的行为。由于是模拟的，对于同一个random(x)总是得到同样的返回值，因此这是一种伪随机。

如果我们想得到一个取值范围在 0-1 之间的 random 函数，可以使用 y = fract(sin(x)*1.0);，只保留小数部分。

系数 1.0

系数 1.0

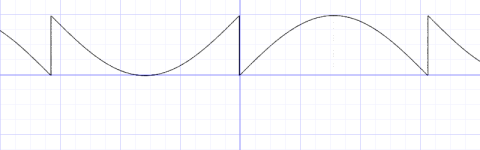
观察这个函数可以发现，如果我们能将周期缩小到极短，对于同一个 x 对应的取值就可以认为是近似随机（伪随机）的。具体方式就是增大系数，例如 y = fract(sin(x)*10.0);

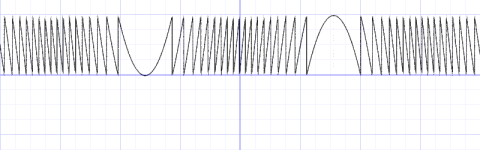
系数 10.0

系数 10.0

进一步增加到 100000，我们已经无法分辨出 sin() 的波形了。再次需要明确一点，不同于 JS 中的 Math.random()，这种方式只是确定性随机，本质其实是一个 Hash 函数。

2维随机

我们需要将 random 应用到 2D 场景中，输入从单一的 x 变成了 xy 坐标，需要将二维向量映射成一个单一值。「the book of shaders」使用了 dot() 内置函数点乘了一个特定的向量，但是并没有解释原因。

float random (vec2 st) {
    return fract(sin(
        dot(st.xy,vec2(12.9898,78.233)))*
        43758.5453123);
}

在网上搜索一番后，找到了这个回答，大概是说最早来自一篇论文，也没有解释选择这三个 Magic Number 的理由。总之生成的效果是很好的，类似黑白电视机的“雪花屏”：

结合之前学到的 Pattern 绘制方法，可以得到更加可控的效果：

vec2 st = gl_FragCoord.xy/u_resolution.xy;
st *= 10.0;
vec2 ipos = floor(st);
vec3 color = vec3(random(ipos));
gl_FragColor = vec4(color,1.0);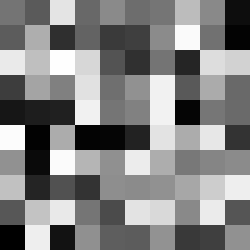

一维噪声

使用我们定义的 random 函数，结合 floor 可以得到阶梯状的函数。

float i = floor(x);
y = random(i);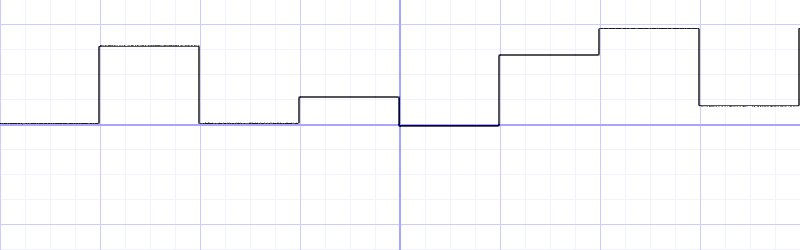

如果我们想对相邻“阶梯”间进行插值，可以使用线性函数或者平滑的插值函数（smoothstep）：

float i = floor(x);
float f = fract(x);
y = mix(rand(i), rand(i + 1.0), f);
// y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));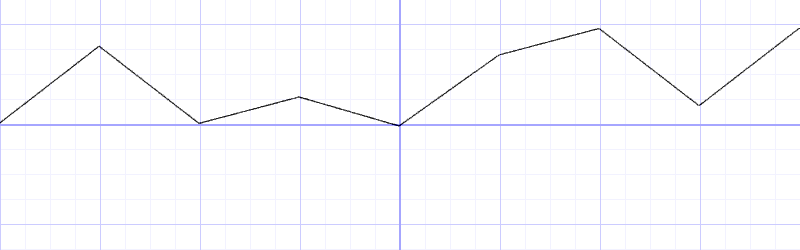

二维噪声

在一维中插值我们选取了 i+1，在二维中进行插值，可以选取相邻的 4 个点。相应的混合函数也需要进行修改。原文中混合函数是展开后的形式，有点难看懂，但是好处是少调用了两次 mix()。

float noise (in vec2 st) {
    vec2 i = floor(st);
    vec2 f = fract(st);

    // Four corners in 2D of a tile
    float a = random(i);
    float b = random(i + vec2(1.0, 0.0));
    float c = random(i + vec2(0.0, 1.0));
    float d = random(i + vec2(1.0, 1.0));

    vec2 u = smoothstep(0.,1.,f);

    // Mix 4 coorners percentages
    return mix(a, b, u.x) +
            (c - a)* u.y * (1.0 - u.x) +
            (d - b) * u.x * u.y;

    // 其实是下面的展开形式
    return mix( mix( a, b , u.x),
                mix( c, d, u.x), u.y);
}

作者在注释中也提到了以上算法来自 shader toy 上，甚至包括了三维中的示例：

其他噪声生成方式

以上生成噪声的方法，都是在随机值之间进行插值，因此被称为 value noise。仔细观察可以发现这种方式生成的结果有明显的块状痕迹，例如下面例子中左侧部分。

当然这种方式的优点就是计算量小，而且在某些场景下已经足够。例如上面例子中的右侧部分，运用了分形布朗运动（Fractal Brownian Motion）

Gradient Noise

在 1985 年 Ken Perlin 开发了另一种 noise 算法 Gradient Noise。Ken 解决了如何插入随机的 gradients（梯度、渐变）而不是一个固定值。这些梯度值来自于一个二维的随机函数，返回一个方向（vec2 格式的向量），而不仅是一个值（float格式）。

具体算法如下，可以看出和 value noise 最大的区别就是使用了 dot() 对四个方向的向量进行插值：

// gradient noise
float noise( in vec2 st ) {
    vec2 i = floor(st);
    vec2 f = fract(st);
	
	vec2 u = smoothstep(0., 1., f);

    return mix( mix( dot( random( i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ), 
                     dot( random( i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
                mix( dot( random( i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ), 
                     dot( random( i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}

Simplex Noise

对于 Ken Perlin 来说他的算法所取得的成功是远远不够的。他觉得可以更好。在 2001 年的 Siggraph 上，他展示了 “simplex noise”

这个算法的改进就十分复杂了，详见2d-snoise-clear

总结

现在我们了解了随机和噪声的基本生成方法，接下来我们需要模拟更多现实中的纹理。

噪声的艺术

CATALOG

噪声函数的基本生成方式