Camera 设计（一）

摄像机操作是任何 3D 渲染引擎必备的功能，正好最近需要实现一个，结合 WebGL Insights 上的文章以及现有开源引擎，总结一下学习所得。本篇集中在四元数的知识上，这部分自己之前完全不了解，强烈推荐阅读 krasjet - quaternion 这篇文章，本文也会大量引用文中内容。

除了常见的矩阵表示，旋转还可以用轴角，欧拉角和四元数表示。尤其是四元数，之前看到 Three.js, Clay.gl 等 3D 引擎都会使用到它，但是一直也没有去尝试理解这种表示方法。这次借着研究摄像机设计问题，了解了它在解决万向节死锁问题和插值问题上的优势。

轴角

首先是比较容易理解的轴角，只需要一根旋转轴和旋转角度，我们就能表示当前的旋转，至于旋转方向，可以使用右手系约定正方向。

但是在实际场景中，尤其是涉及到一组连续旋转，由于调整旋转顺序会影响到最终的结果，很难将轴角的叠加表示成“加法”。

欧拉角

欧拉角理解起来要更直观，因为更加贴近我们在日常生活中的描述，比如摄像机运动（tilt pan…），水平坐标系（也称作地心坐标系）中的经纬度。

但欧拉角的问题是需要约定三个坐标轴的执行顺序。比如 Three.js 中欧拉角转换到四元数的方法就需要考虑全部六种组合：Quaternion.js#L225-L260。再比如 Unity 约定了欧拉旋转的旋转顺序是Z、X、Y（来自「【Unity技巧】四元数（Quaternion）和旋转」）。

以及著名的 Gimbal Lock 万向节死锁问题。这篇「游戏动画中欧拉角与万向锁的理解」中举了一个手机的例子，跟着操作之后能有切身体会。

最后在实现中三个轴欧拉角旋转也是通过三个旋转矩阵相乘实现的，效率比较低。

四元数

这次关于四元数的学习主要来自「quaternion」。一些基本定义和公式推导完全可以阅读这篇文章（62p 还是挺长的）。

首先是基本运算，来自 gl-matrix，尤其是两个四元数相乘，就可以表示两个旋转动作的叠加，在后面可以看到它的便利：

quat.add = vec4.add;
// Graßmann 积
quat.multiply = function (out, a, b) {
    var ax = a[0], ay = a[1], az = a[2], aw = a[3],
        bx = b[0], by = b[1], bz = b[2], bw = b[3];

    out[0] = ax * bw + aw * bx + ay * bz - az * by;
    out[1] = ay * bw + aw * by + az * bx - ax * bz;
    out[2] = az * bw + aw * bz + ax * by - ay * bx;
    out[3] = aw * bw - ax * bx - ay * by - az * bz;
    return out;
};

然后是一个四元数的逆和共轭：

// 求逆
quat.invert = function (out, a) {
    var a0 = a[0], a1 = a[1], a2 = a[2], a3 = a[3],
        dot = a0 * a0 + a1 * a1 + a2 * a2 + a3 * a3,
        invDot = dot ? 1.0 / dot : 0;
    out[0] = -a0 * invDot;
    out[1] = -a1 * invDot;
    out[2] = -a2 * invDot;
    out[3] = a3 * invDot;
    return out;
};
// 如果是单位四元数，逆就是共轭
quat.conjugate = function (out, a) {
    out[0] = -a[0];
    out[1] = -a[1];
    out[2] = -a[2];
    out[3] = a[3];
    return out;
};

这样我们就能通过四元数描述 3D 旋转：

双倍覆盖

关于四元数和 3D 旋转的关系，这里直接引用上面 PDF 的 3.5 小节：

因此，q 和 -q 对应的是同一个旋转矩阵。下面我们来看一下从轴角，欧拉角，旋转矩阵到四元数的转换公式，在各种工具库和 3D 引擎中都能在封装好的 Quaternion 类中都能看到。

轴角，欧拉角，旋转矩阵的转换

例如我们想把一个四元数绕 X 轴旋转一个角度，得到一个新的四元数。首先将欧拉角转换到四元数，可以参考eulerToQuaternion。值得一提的是这个网站各种推导过程十分详细，从 Three.js 中源码的注释可以看出它的实现也是参考了该网站的公式推导，例子。

根据公式，要计算 w = c1 c2 c3 - s1 s2 s3，此时绕 X 轴旋转，c2 = c3 = 1，s2 = s3 = 0。最终这个四元数可以表示为（0, s1, 0, c1），和原四元数相乘，就能得到结果四元数：

quat.rotateX = function (out, a, rad) {
    rad *= 0.5;

    var ax = a[0], ay = a[1], az = a[2], aw = a[3],
        // 欧拉角对应的四元数：(0, s1, 0, c1）
        bx = Math.sin(rad), bw = Math.cos(rad);

    // 四元数相乘，Graßmann 积
    out[0] = ax * bw + aw * bx;
    out[1] = ay * bw + az * bx;
    out[2] = az * bw - ay * bx;
    out[3] = aw * bw - ax * bx;
    return out;
};

轴角和旋转矩阵到四元数的转换也都可以参考公式实现：

// 轴角到四元数
// http://www.euclideanspace.com/maths/geometry/rotations/conversions/angleToQuaternion/index.htm
quat.setAxisAngle()

// 旋转矩阵到四元数
quat.fromMat3()
// 从四元数得到旋转矩阵
mat3.fromQuat()

现在我们可以看 nucleo 中摄像机操作的一个使用例子，将 XYZ 的三个轴角分别转换成四元数，最终得到旋转矩阵，实现摄像机的旋转效果：

// Camera.TYPE.EXPLORING

var rotX = quat.setAxisAngle(quat.create(), [1, 0, 0], -elevation * nucleo.define.DEG_2_RAD);
var rotY = quat.setAxisAngle(quat.create(), [0, 1, 0], -azimuth * nucleo.define.DEG_2_RAD);
var rotZ = quat.setAxisAngle(quat.create(), [0, 0, 1], roll * nucleo.define.DEG_2_RAD);
var rotQ = quat.multiply(quat.create(), rotY, rotX);

rotQ          = quat.multiply(quat.create(), rotQ, rotZ);
var rotMatrix = mat4.fromQuat(mat4.create(), rotQ);
mat4.translate(this._matrix, this._matrix, [0, 0, -this._distance]);
mat4.multiply(this._matrix, this._matrix, rotMatrix);
mat4.translate(this._matrix, this._matrix, [0, 0, this._distance]);

四元数插值

在实现动画时，我们经常需要根据时间获取一个变换的中间状态，也就是插值。那么对于两个四元数，如何表示这两个旋转变换的中间状态呢？

Slerp

因为对⻆度线性插值直接是让向量在球面上的一个弧上旋转，所以又称球面线性插值 ( Spherical Linear Interpolation)，或者「Slerp」．类比于 Lerp 是平面上的线性插值，Slerp 是球面上的线性插值。

这里直接引用 krasjet - quaternion 中的内容：

很容易得到第一版插值公式，很容易带入 t = 0 和 t = 1 进行验证： \begin{array}{l} q_{t} = Slerp(q_{0}, q_{1};t) = (q_{1}q_{0}^{*})^{t}q_{0} \end{array}

但是很明显这个公式涉及幂运算，不够高效。实际使用的 Slerp 公式推导过程可以参考上面的 pdf，总共需要一个反三角函数和三个三角函数运算，相比幂运算要高效的多： \begin{array}{l} θ = cos^{−1}(q_{0} · q_{1}) \end{array} \begin{array}{l} q_{t} = Slerp(q_{0}, q_{1},t) =\frac{sin((1 − t)θ)}{sin(θ)}q_{0} +\frac{sin(tθ)}{sin(θ)}q_{1} \end{array}

如果两个四元数之间的夹角很小，需要使用 Nlerp 线性插值，原因有两个：角度很小的情况下 Nlerp 和 Slerp 效果近似，另外由于计算精度问题，sin作为分母会出现除以 0 的错误。要注意 Nlerp 最终返回时需要转成单位四元数：

// https://github.com/mrdoob/three.js/blob/master/src/math/Quaternion.js#L561-L569

if ( sqrSinHalfTheta <= Number.EPSILON ) {
    var s = 1 - t;
    this._w = s * w + t * this._w;
    this._x = s * x + t * this._x;
    this._y = s * y + t * this._y;
    this._z = s * z + t * this._z;
    // 转成单位四元数
    return this.normalize();
}

另外，之前我们已经知道 q 与 −q 描述的是同一个旋转，所谓“双倍覆盖”。

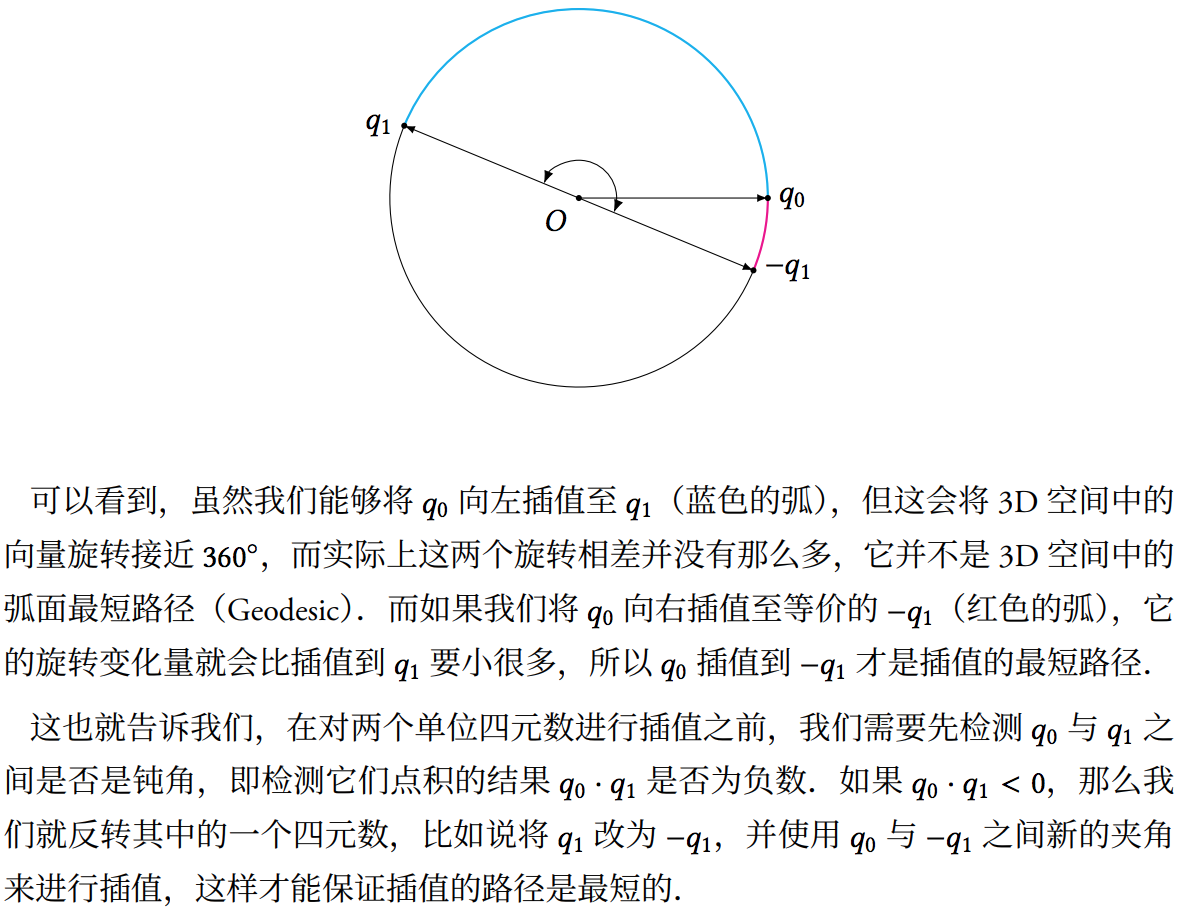
// https://github.com/mrdoob/three.js/blob/master/src/math/Quaternion.js#L531-L542

var cosHalfTheta = w * qb._w + x * qb._x + y * qb._y + z * qb._z;
if ( cosHalfTheta < 0 ) {
    this._w = - qb._w;
    this._x = - qb._x;
    this._y = - qb._y;
    this._z = - qb._z;

    cosHalfTheta = - cosHalfTheta;
}

Squad

如果我们需要对多个四元数进行插值，对每一对四元数使用 Slerp 插值虽然能够保证每两个四元数之间的⻆速度是固定的，但是⻆速度会在切换插值四元数时出现断点，或者说在切换点不可导。于是，Shoemake 在 1987 年提出了一个更高效的近似算法，也就是我们熟悉的 Squad。向量的 Squad 算法叫做 Quad，代表「Quadrangle」。与三次 Bézier 曲线嵌套了三层一次插值不同，Quad 使用的是一层二次插值嵌套了一层一次插值。

\begin{array}{l} Squad(q_{0}, q_{1}, q_{2}, q_{3};t) = Slerp(Slerp(q_{0}, q_{3};t), Slerp(q_{1}, q_{2};t); 2t(1 − t)) \end{array}

具体实现如下，以 Three.js 为例：

var squad = function (q1, qr1, qr2, q2, h) {
    var s1 = THREE.Quaternion.slerp(q1, q2, new THREE.Quaternion(), h);
    var s2 = THREE.Quaternion.slerp(qr1, qr2, new THREE.Quaternion(), h);
    var sh = 2 * h * (1 - h);
    return THREE.Quaternion.slerp(s1, s2, new THREE.Quaternion(), sh);
};

Quad（右侧）减少了 Lerp 次数，但是效果已经很近似 Bézier（左侧）了：

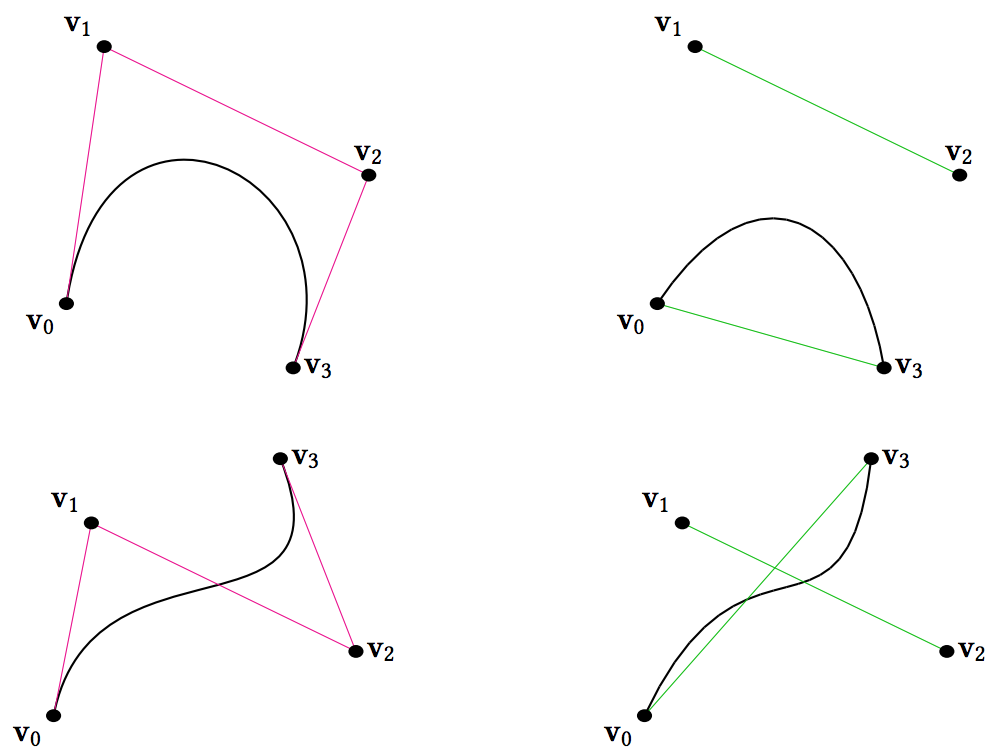
对于一组四元数中每一对相邻的两个，都可以应用 Squad，但是需要找到中间的控制点： \begin{array}{l} Squad(q_{i},s_{i},s_{i+1}, q_{i+1};t) = Slerp(Slerp(q_{i}, q_{i+1};t), Slerp(s_{i},s_{i+1};t); 2t(1 − t)) \end{array} \begin{array}{l} s_{i} = q_{i}exp(−\frac{log(q_{i}^{*}q_{i-1})+log(q_{i}^{*}q_{i+1})}{4}) \end{array}

具体实现如下，以 Three.js 为例：

var quadrangle = function (qprev, qcurr, qnext) {
    var iQcQn = new THREE.Quaternion().copy(qcurr).inverse().multiply(qnext);
    var iQcQp = new THREE.Quaternion().copy(qcurr).inverse().multiply(qprev);
    var l = factor(-1/4, add(log(iQcQn), log(iQcQp)));
    return new THREE.Quaternion().copy(qcurr).multiply(exp(l));
};

最终我们来看一个 Three.js 例子，执行一组连续的旋转，略微修改自gist - bellbind/1702547：

See the Pen Three.js with quaternion squad by xiaop (@xiaoiver) on CodePen.

总结

以上就是部分涉及旋转的四元数知识了，后续我们会在 Camera 设计中大量使用到。

Camera 设计（一）

CATALOG

了解四元数

轴角

欧拉角

四元数

双倍覆盖

轴角，欧拉角，旋转矩阵的转换

四元数插值

Slerp

Squad

总结

参考资料