思路 & PCF
给场景中光照下的物体增加阴影能够显著增强“真实感”,即使阴影并不十分完美。 在光线追踪算法中,实现阴影(shadow ray)更加符合直觉。而在光栅化算法中,基于 Shadow Map 的实现是最常见的。下面的内容主要来自:
- 《Real-Time Shadows》
- 《Real-Time Rendering 3rd》第九章全局光照 9.1 节
- Bavoil 在 GDC08 上的演讲:Soft Shadow Mapping
在阅读学习这些具体实现方法的过程中,也接触到了一些统计学和信号处理方面的知识,个人觉得收获还是很大的。
可以访问在线 Demo 地址查看不同实现的效果。也可以访问项目 Github 地址查看源码。
阴影的“软硬”
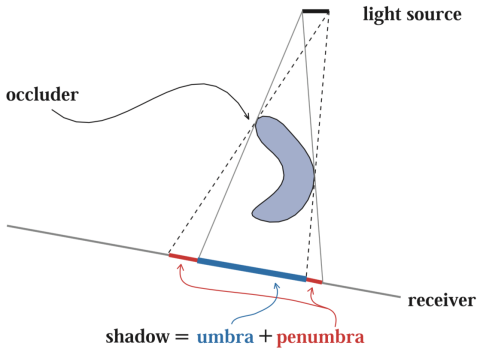
在下面的图中,a 点与光源之间没有任何物体阻挡,因此是照亮(lit)的。而地面也就是接受者(receiver)上的 c 点被遮挡者(occluder)立方体遮挡,处于本影区(umbra)。b 点处于被部分遮挡形成的半影区(penumbra)。
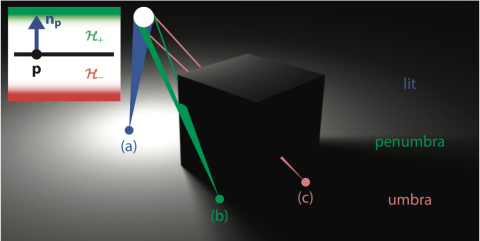
理想中的点光源会造成只有本影区的硬阴影(hard shadows),但是现实中的光源毕竟本身有体积,会形成拥有半影区的软阴影(soft shadows)。两者的关系不是简单地将硬阴影的边缘模糊化处理就能得到软阴影,根据我们日常生活中的经验,光源和接受者的距离越近,软阴影的边缘就越清晰(软度降低)。
Shadow Map 思路
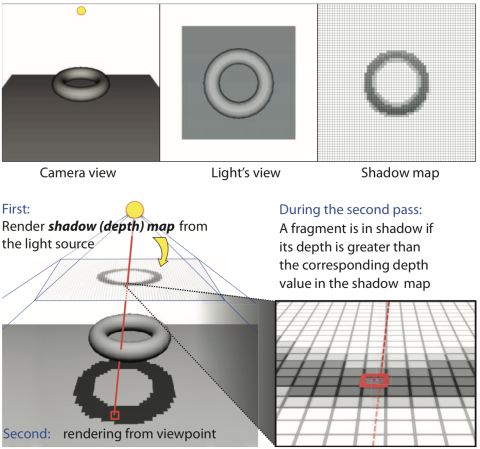
来自《Real-Time Shadows》中的一张图总结的十分清晰,由于光栅化的渲染管线相比基于光线追踪的实现方式缺少全局性信息,每个 fragment 并不清楚全局的光照情况,无法直接判断自己是否处于阴影中,因此需要额外预渲染阶段。 第一次渲染中以光源位置作为视点,基于 Z-buffering 算法,将每个像素点的深度值(z-depth)也就是距离光源最近的对象距离记录在 Z-buffer 中,输出到 FBO(Framebuffer Object) 关联的 texture 中,生成 Shadow Map。 第二次场景渲染时,以正常摄像机作为视点,将每个 fragment 到光源的距离和 Shadow Map 中保存的深度值进行比较,如果大于后者则说明被其他物体遮挡处于阴影之中。
整体思路就是这样,针对不同的光源类型有一些额外的注意点,比如:
- 平行光(Directional Light)并不存在确定的光源位置,在投影矩阵的选择上应该采用平行投影而非透视投影
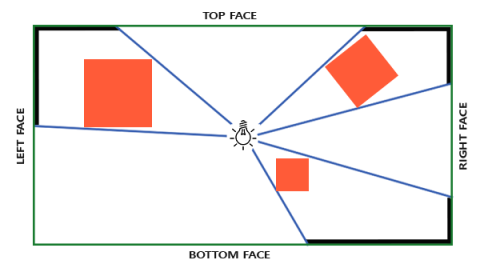
- 平行光和聚光灯(Spot Light)都有固定的方向,而泛光灯(omnidirectional shadow maps)向四面八方发光。其实思路都是一致的,只是具体使用 Cubemap 保存 Shadow Map,可以参考 learnopengl.com - Point-Shadows
我自己实现的 Demo 使用的是聚光灯这种相对简单的场景。
基础版本
有了以上思路,我们很容易使用 WebGL 实现,涉及到具体 API 的使用例如 FBO 等等可以参考之前的一篇《创建阴影 - WebGL Programing Guide 笔记》,后续就只关注 Shader 中的细节了。其中第一对 Shadow Shader 负责计算光源到物体的距离,而第二对 Display Shader 负责真正的场景绘制。
在 Shadow Fragment Shader 中,将深度值储存在 R 分量里,其实 RGBA 任何一个分量都可以。
precision mediump float;
void main() {
gl_FragColor = vec4(gl_FragCoord.z, 0.0, 0.0, 0.0);
}在 Display Fragment Shader 中,首先需要转换到 NDC(通过除以 w 分量得到)。
其次 texture 坐标取值范围是 [0,1],从 NDC [-1,1] 转换而来时需要除以 2 再加 0.5。
最后比较当前 fragment 到光源的距离和 shadow map 中对应的深度值,判断是否处于阴影中。
float calcShadow(sampler2D depths, vec4 positionFromLight, vec3 lightDir, vec3 normal) {
// Clipped Coord -> NDC -> texture Coord
vec3 shadowCoord = (positionFromLight.xyz / positionFromLight.w) * 0.5 + 0.5;
// 获取 shadow map 中保存的深度值
vec4 rgbaDepth = texture2D(depths, shadowCoord.xy);
// 比较当前距离和深度值
return step(shadowCoord.z, rgbaDepth.r);
}这个最基础的版本存在一些明显的问题,让我们来看一下。
精度问题
运行 Demo 会发现根本没有阴影生成,这是为啥呢?
显而易见的,当物体到光源的距离过远时,使用 RGBA 中任何一个分量存储深度值都会存在精度丢失问题,毕竟只有 1 byte。 合适的做法是在 Shadow Fragment Shader 中充分利用四个分量也就是 4 bytes 存储。
precision mediump float;
void main() {
vec4 bitShift = vec4(1.0, 256.0, 256.0 * 256.0, 256.0 * 256.0 * 256.0);
const vec4 bitMask = vec4(1.0/256.0, 1.0/256.0, 1.0/256.0, 0.0);
vec4 rgbaDepth = fract(gl_FragCoord.z * bitShift);
rgbaDepth -= rgbaDepth.gbaa * bitMask;
gl_FragColor = rgbaDepth;
}而在 Display Fragment Shader 中获取原始深度值只需要通过如下方式: \begin{array}{l} depth = rgbaDepth.r \times 1.0 + \frac{rgbaDepth.g}{256.0} + \frac{rgbaDepth.b}{256.0 \times256.0 } + \frac{rgbaDepth.a}{256.0 \times256.0\times256.0 } \end{array}
以上运算可以通过 dot() GLSL 内置函数完成:
float unpackDepth(const in vec4 rgbaDepth) {
const vec4 bitShift = vec4(1.0, 1.0/256.0, 1.0/(256.0*256.0), 1.0/(256.0*256.0*256.0));
float depth = dot(rgbaDepth, bitShift);
return depth;
}最后我们定义我们的阴影效果比较函数,后续这个方法都不会再发生改变:
float texture2DCompare(sampler2D depths, vec2 uv, float compare) {
float depth = unpackDepth(texture2D(depths, uv));
return step(compare, depth);
}至少现在阴影能显示出来了,让我们来看下一个问题。
深度偏移问题
再次运行我们的 Demo 发现物体表面居然也出现了阴影,如同一颗复活节彩蛋,这又是咋回事呢?

这种现象也被称作 Surface acne 或者 self-shadowing,原因是 Shadow Map 的分辨率是离散的,多个 fragment 会对应到同一个纹素,增加 Shadow Map 的分辨率(我们的 Demo 采用的是 2048 * 2048)只能减少可能性,并不能完全避免这个问题。 比如下图中一个倾斜的表面,蓝色的点和红色的点都对应 Shadow Map 中的同一个纹素,但是蓝色点距离光源的距离更远,因此在比较时被错误地认为处于阴影中。 常用的解决办法是给 Shadow map 中保存的深度值增加一个偏移值(Depth bias):
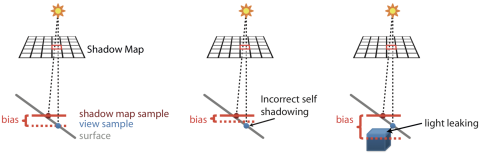
但是,这个偏移值过大又会出现“Peter Pan”现象(物体似乎飘在了空中),也叫漏光(light leaking),如下图右边所示,本该处于阴影的区域反而被照亮了。

所以这个偏移值的选择十分重要,如果采用一个固定值例如 0.005,当表面法线与光源方向夹角很大(上图中表面更加倾斜)时还是会出现,更好的做法是根据法线方向和光线方向计算:
float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
float texture2DCompare(sampler2D depths, vec2 uv, float compare, float bias){
float depth = unpackDepth(texture2D(depths, uv));
return step(compare - bias, depth);
}勾选 Demo 中“shadow-high-precision”可以查看目前的效果,很容易发现块状痕迹让阴影显得很不自然,而且完全没有半影区。

走样问题
锯齿状的痕迹也被称作走样(Aliasing),原因其实和之前 Surface acne 的问题一样。在下图中橙色区域内的所有 fragment 都对应到了 Shadow Map 中的同一个纹素。实时渲染中的软阴影技术也有相应的解释。
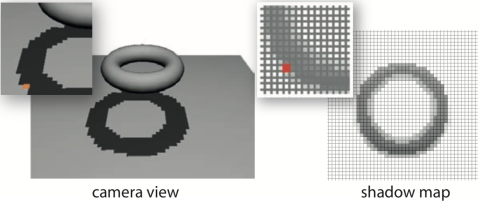
分析图像走样和反走样,尤其是结合一些实际例子,可以阅读这篇走样与反走样。
反走样或者更熟悉的名字–“抗锯齿”就是为了解决这个问题。 要注意,下面介绍的方法都不能生成真正物理意义上的软阴影,它们针对的其实都是走样问题,目的是平滑/模糊阴影的边界。
PCF
首先需要介绍一些术语和标记,主要来自《Real-Time Shadows》:
- 滤波:图像处理中可以通过滤波强调一些特征或者去除图像中一些不需要的部分。滤波是一个邻域操作算子,利用给定像素周围的像素的值决定此像素的最终的输出值,在我们的场景中就是使用 Shadow Map 中的部分采样点计算每个 fragment 的阴影效果
- 滤波核函数 :图像处理中对滤波核和图像应用卷积操作,可以得到常见的模糊,锐化等效果。可以参考卷积矩阵
- 深度函数 :t 就是 Shadow Map 纹理坐标, 表示该坐标对应的深度值
- 参考深度值 :fragment 到光源的距离
- 阴影比较函数 :这是一个单位阶跃函数
对深度信号 滤波是无效的,因为最终阶梯函数 的结果还是是二分的,走样问题依然存在。 \begin{array}{l} f_{filter}^{blur}(t,\tilde{z})=H(\sum_{t_{i}\in K}k(t_{i}-t)z(t_{i})-\tilde{z}) \end{array}
而 PCF(Percentage Closer Filtering)直接对阴影信号 进行滤波,就可以实现平滑阴影边缘的效果: \begin{array}{l} f_{filter}^{pcf}(t,\tilde{z})=\sum_{t_{i}\in K}(k(t_{i}-t)H(z(t_{i})-\tilde{z})) \end{array}
从公式中可以看出影响阴影效果的决定因素就是滤波核函数 以及采样数 。下面我们就介绍几种不同的 PCF 实现。
最近邻采样
最简单的滤波核函数肯定是 Box Filter,图像处理中也称作均值滤波。一个采样点的值由周围若干个采样点平均而来。Shadow Map 中的一个纹素除了自身,周围相邻的多个纹素都要参与计算。如下图所示:
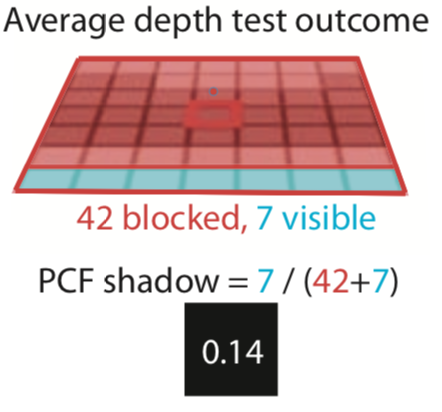
首先我们需要计算一个纹素的大小(texelSize),比如 Demo 中使用的 Shadow Map 分辨率是 2048 * 2048:
vec2 texelSize = vec2(1.0) / vec2(2048.0, 2048.0);然后选取滤波核的尺寸,我们的 Demo 中选择 5*5,那么就可以简单计算出每个 fragment 的阴影效果:
float PCF(sampler2D depths, vec2 uv, float compare, float bias) {
float result = 0.0;
for (int x = -2; x <= 2; x++) {
for (int y = -2; y <= 2; y++) {
vec2 off = texelSize * vec2(x,y);
result += texture2DCompare(depths, uv + off, compare, bias);
}
}
return result / 25.0;
}这种方法的问题很明显,对选取的 n*n 滤波核,由于权重都是平均的,因此最终计算出来的阴影效果只有 n^2+1 种取值,因此条状痕迹明显。 并且为了得到较好的效果,需要增大滤波核尺寸,相应地也就增加了运算量。我们的 Demo 效果如下:

双线性插值
为了解决块状痕迹,我们很容易联想到纹理过滤中使用 GL_NEAREST 和 GL_LINEAR 方法的区别:

这里我们同样可以使用双线性插值。例如下图中使用四个红点计算 P 的值:先沿 x 轴方向计算两个蓝点,再沿 y 轴方向计算 P 点,顺序反过来结果也是一样。
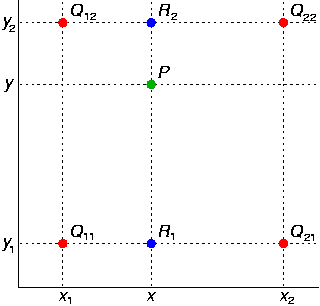
具体可以参考 THREE.JS 的实现,获取左下左上右下右上 4 个纹素的阴影值,也就是上图中的四个红点,这里使用了 glsl 内置 mix() 函数进行插值:
float texture2DShadowLerp(sampler2D depths, vec2 uv, float compare, float bias){
float size = 2048.0;
vec2 centroidUV = floor(uv * size + 0.5) / size;
vec2 f = fract(uv * size + 0.5);
float lb = texture2DCompare(depths, centroidUV + texelSize * vec2(0.0, 0.0), compare, bias);
float lt = texture2DCompare(depths, centroidUV + texelSize * vec2(0.0, 1.0), compare, bias);
float rb = texture2DCompare(depths, centroidUV + texelSize * vec2(1.0, 0.0), compare, bias);
float rt = texture2DCompare(depths, centroidUV + texelSize * vec2(1.0, 1.0), compare, bias);
float a = mix(lb, lt, f.y);
float b = mix(rb, rt, f.y);
float c = mix(a, b, f.x);
return c;
}相比之下不需要太大的滤波核,但是总的计算量未必减少了:
float PCFLerp(sampler2D depths, vec2 uv, float compare, float bias) {
float result = 0.0;
for(int x = -1; x <= 1; x++){
for(int y = -1; y <= 1; y++){
vec2 off = texelSize * vec2(x,y);
result += texture2DShadowLerp(depths, uv + off, compare, bias);
}
}
return result / 9.0;
}勾选 Demo 中的“shadows-pcf-lerp”,可以看到之前明显的条带状痕迹缓解了很多:

Poisson Disk
过于规律的块状痕迹还可以采用随机采样的方法缓解。但是同样都是随机,效果也有差别,例如下图中右侧使用 Poisson Disk 采样集使得两个采样点间距不会太近,相较左侧完全随机的采样,效果又要显得规整一些:
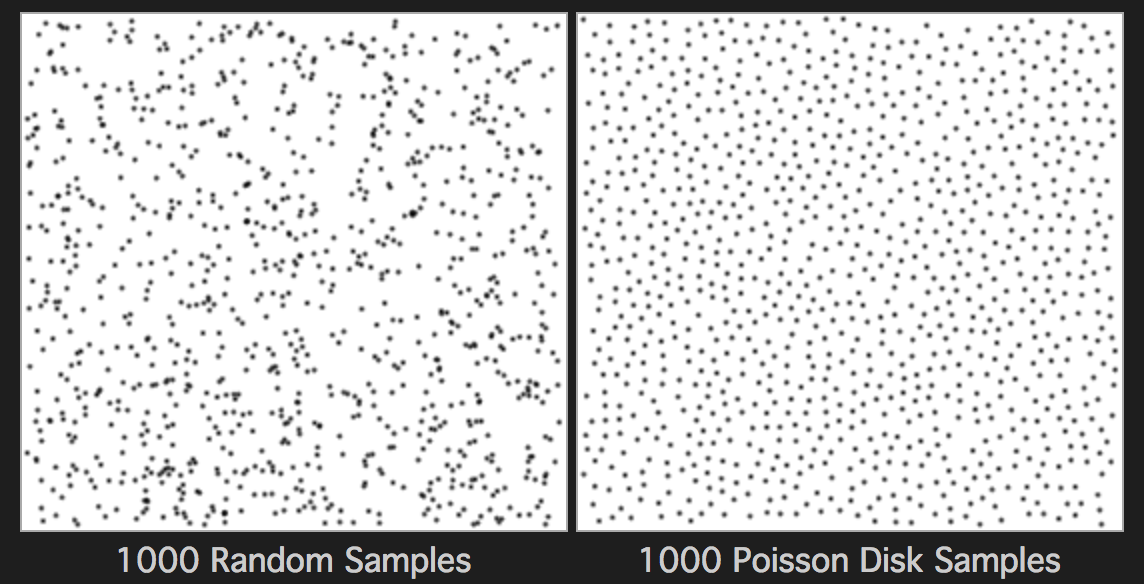
如果对生成 Poisson Disk 采样集的算法和具体实现感兴趣,可以参考这两篇文章:文章1,文章2以及 Youtube 上的视频。我们这里就直接使用生成好的结果例如 4 个采样点,来自 Babylon.js,并传入 shader uniform 变量 uPoissonDisk 中:
const poissonDisk = [
-0.94201624, -0.39906216,
0.94558609, -0.76890725,
-0.094184101, -0.92938870,
0.34495938, 0.29387760
];这次我们选取了更小的 2*2 的滤波核,把 Poisson Disk 采样点坐标作为偏移量:
uniform float uPoissonDisk[8];
float PoissonDisk(sampler2D depths, vec2 uv, float compare, float bias) {
float result = 0.0;
for (int i = 0; i < 4; i++) {
result += texture2DCompare(depths, uv + vec2(uPoissonDisk[i * 2], uPoissonDisk[i * 2 + 1])/2048.0, compare, bias);
}
return result / 4.0;
}Demo 效果如下,可以勾选“shadows-poisson-disk”查看,我们发现效果几乎和使用最近邻采样 5*5 差不多,虽然还是有条状痕迹:

Stratified Poisson Disk
我们发现在滤波核计算时,每个纹素的偏移量还是固定的,使用随机值是否能缓解这些“规律”的条状痕迹呢?
在之前「噪声的艺术」一文中我们介绍了 GLSL 中实现伪随机函数的方法:
float random(vec3 seed, int i) {
vec4 seed4 = vec4(seed,i);
float dot_product = dot(seed4, vec4(12.9898,78.233,45.164,94.673));
return fract(sin(dot_product) * 43758.5453);
}这里我们可以使用更多的 Poisson Disk 采样点(16个),来自 opengl-tutorials,同时采用随机选取偏移量的方式。这里有一点需要注意,WebGL 中除了 for 循环这些情况不允许使用动态变量作为数组下标,因此我们采用了一种 Hack 的方法:
uniform float uPoissonDisk[32];
float StratifiedPoissonDisk(sampler2D depths, vec2 uv, float compare, float bias) {
float result = 0.0;
for (int i = 0; i < 4; i++) {
// 根据每个像素点的位置生成随机值
int index = int(mod((16.0 * random(floor(v_Position.xyz * 1000.0), i)), 16.0));
// WebGL 中不允许使用动态变量作为数组下标,无法直接使用 uPoissonDisk[index * 2]
for (int j = 0; j < 16; j++) {
if (j == index) {
result += texture2DCompare(depths, uv + vec2(uPoissonDisk[j * 2], uPoissonDisk[j * 2 + 1])/2048.0, compare, bias);
break;
}
}
}
return result / 4.0;
}条状痕迹是缓解了,但是带来的是明显的噪声。用 GDC08 Soft Shadow Mapping 中的一句话总结就是 “Trades banding for noise”。

Rotated Poisson Disk
除了定义更多的 Poisson Disk 采样点来实现,我们还可以在保持采样点不变(依然是4个)的基础上,每次旋转一个随机角度得到随机的采样点:
uniform float uPoissonDisk[8];
float RotatedPoissonDisk(sampler2D depths, vec2 uv, float compare, float bias){
float result = 0.0;
for (int i = 0; i < 4; i++) {
// 随机角度
float angle = 2.0 * PI * random(floor(v_Position.xyz * 1000.0), i);
float s = sin(angle);
float c = cos(angle);
// 旋转矩阵
vec2 rotatedOffset = vec2(uPoissonDisk[i * 2] * c + uPoissonDisk[i * 2 + 1] * s,
uPoissonDisk[i * 2] * -s + uPoissonDisk[i * 2 + 1] * c);
result += texture2DCompare(depths, uv + rotatedOffset/2048.0, compare, bias);
}
return result / 4.0;
}效果和 Stratified Poisson Disk 是差不多的,使用更少的 Poisson Disk 采样点,但是运算量增加。同样的,可见的噪声问题依然存在:

PCF 存在的问题
不难发现 PCF 的一个很大的问题就是当滤波核尺寸变大,在计算每个 fragment 的阴影效果时,都需要 Shadow Map 中更多采样点的参与,进行一次完整的滤波核函数的计算。无法进行预计算的原因是 依赖 。有两种思路解决这个问题:
- 解构 ,使其连续化且不依赖 ,这样就可以进行预计算。代表方法有 CSM(Convolution Shadow Mapping)和 ESM(Exponential Shadow Mapping)。
- 不再使用信号处理中的卷积计算滤波核数据,转而从统计角度考虑这个问题,使用灰度值来表达阴影效果。代表方法就是 VSM(Variance Shadow Mapping)。
另外,PCF 虽然能对阴影进行平滑模糊,但毕竟无法模拟基于物理的软阴影, PCSS(Percentage Closer Soft Shadows)能够设置变化的滤波核来改进这一点。
总结
现在我们了解了 Shadow Map 的基本思路以及 PCF 的实现及缺陷。下一部分中我们将学习更多实现方法: CSM ESM 和 VSM。 另外,可以访问在线 Demo 地址查看不同实现的效果,放大可以看到更多阴影细节。 最后,本人也是慢慢学习图形学的一个前端开发者,本文以及后续文章中有任何的错误都十分欢迎指正。
参考资料
- Real-Time Shadows,对应的中文译本《实时阴影技术》
- Real-Time Rendering,浅墨的第三版读书笔记很棒
- GDC08 Soft Shadow Mapping
- 实时渲染中的软阴影技术
- Point-Shadows - learnopengl.com
- soft-shadow-mapping
- GPU Gems
- Improvements for shadow mapping in OpenGL and GLSL
- OpenGL Tutorial 16: Shadow mapping
- Poisson Disk Sampling
- VSM 实现

